Monochrome Image

Intensity

I(x, y)

Intensity (grey level) of the image at point (x, y).

  • Amount of source light incident on the scene
  • Amount of light reflected by the objects in the scene

Digitizing an Image

When x, y, and I(x, y) are finite & discrete quantities, the image is a digital image.

  • Digitizing coordinates: sampling
  • Digitizing intensity values: quantization

Representation

$$ I(i, j) = \begin{bmatrix}

I{0,0} & \dots & I{0, M-1} \ \vdots & \ddots & \vdots \ I{N-1,0} & \dots & I{n-1, M-1} \

\end{bmatrix}

$$

Quality

  • Spatial resolution
    • $$N \times M$$
    • Problem
      • Sampling checkerboards
  • Gray-level resolution
    • 256: 8-bit image
    • Problem
      • False contouring

Pixel

Neighbor

Pixel p at (x, y).

  • 4-neighbors $$N_4(p)$$
  • Diagonal neighbors $$N_D(p)$$
  • 8-neighbors $$N_8(p)$$

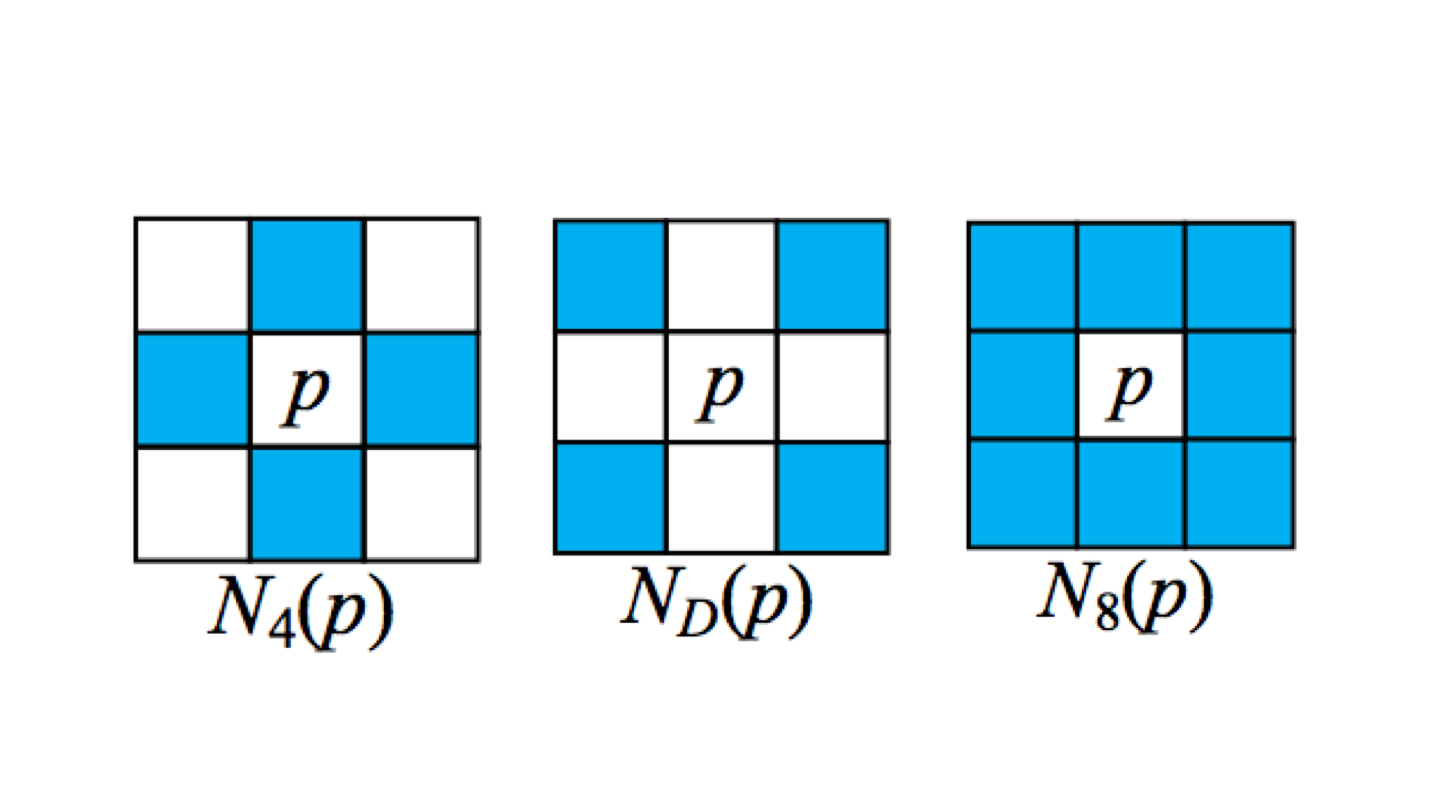
Adjacency

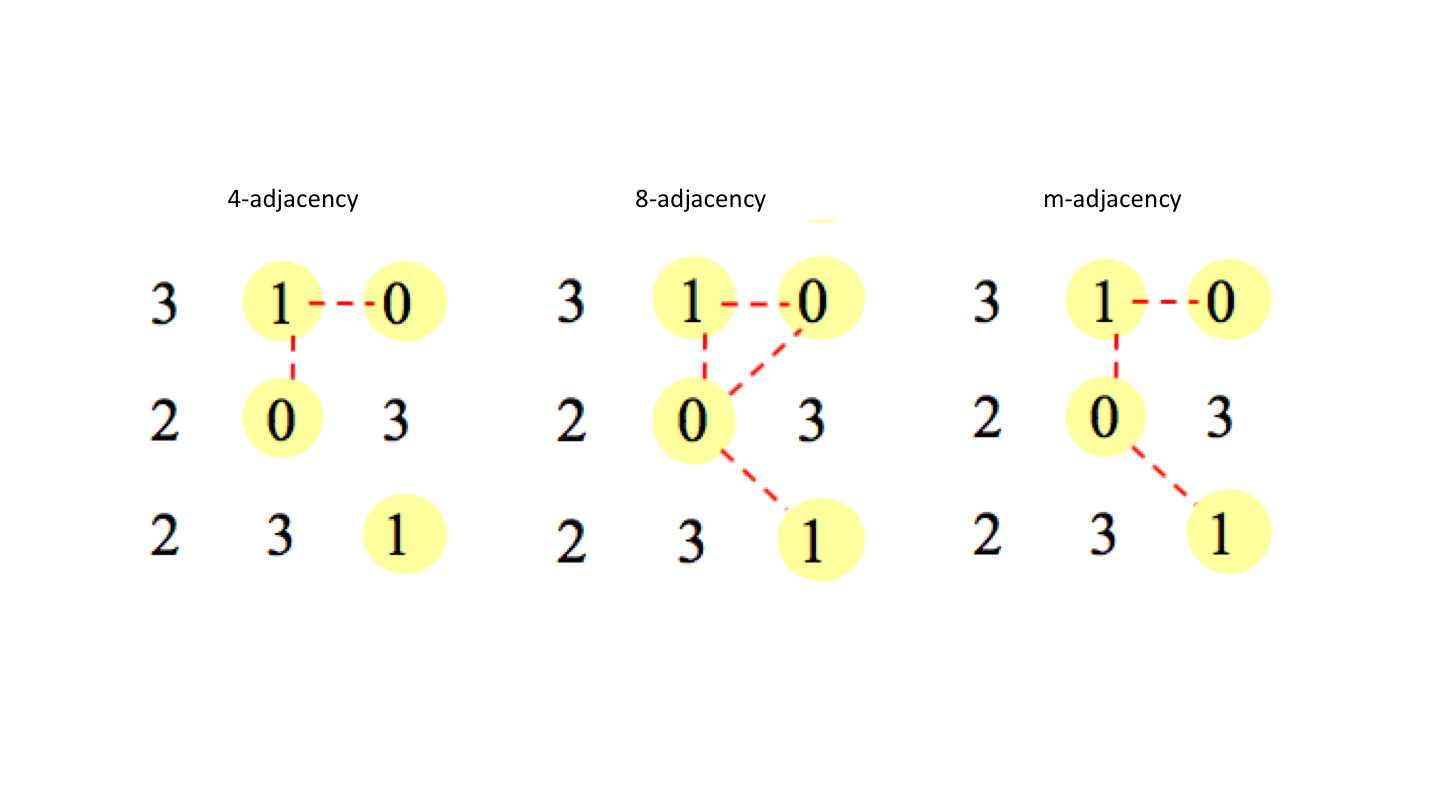
Set of gray-level values V for defining adjacency.

  • 4-adjacent
    • q in set $$N_4(p)$$
  • 8-adjacent
    • q in set $$N_8(p)$$
  • m-adjacent
    • q in set $$N_4(p)$$
    • q in set $$N_D(p)$$ and set $$N_4(p) \cap N_4(q)$$ has no pixels with values from V

Set Adjacency

2 image subsets $$S_1$$ and $$S_2$$ are adjacent if some pixel in $$S_1$$ is adjacent to some pixel in $$S_2$$.

  • 4-adjacent
    • Implies 8-adjacent & m-adjacent
  • 8-adjacent
    • Doesn't imply m-adjacent
  • m-adjacent

Path

A sequence of pixels where $$(xi, y_i)$$ and $$(x{i-1}, y_{i-1})$$ are adjacent.

  • Length n for n+1 pixels
  • Closed if $$(x_0, y_0) = (x_n, y_n)$$

Connectivity

A set of pixels S.

  • Connected
    • There exists a path between p and q consisting entirely of pixels in S
  • Connected component
    • The set of pixels mutually adjacent in S
      • 4-adjacent
      • 8-adjacent
        • Implies m-adjacent
      • m-adjacent
  • Connected set
    • If S has only 1 connected component

Distance

  • Distance function D
    • For pixels p, q, z at the corners of a triangle:
      • $$D(p, q) \ge 0$$
      • $$D(p, q) = 0$$ iff $$p = q$$
      • $$D(p, q) = D(q, p)$$
      • $$D(p, z) \le D(p, q) + D(q, z)$$
  • Measures
    • Euclidean distance
      • $$D_e(p, q) = \sqrt{(x - s)^2 + (y - t ^2)}$$
    • $$D_4$$ distance (city-block distance)
      • $$D_4(p, q) = |x - s| + |y - t|$$
    • $$D_8$$ distance (chessboard distance)
      • $$D_8(p, q) = max(|x - s|, |y - t|)$$
    • $$D_m$$ distance
      • Length of shortest m-path

Logic Operations

  • Negative transformation
    • NOT
  • Masking / region of interest (ROI) processing: selecting sub-images in an image
    • AND
    • OR

Arithmetic Operations
  • Image averaging
    • Addition & division
    • Usage
      • Noise reduction
        • Remove zero-mean uncorrelated noise
        • $$\begin{aligned}\bar{g}(x, y) &= \frac{1}{K} \sum^{K-1}{i=0} g_i(x, y) \ &= \frac{1}{K} \sum^{K-1}{i=0} [f(x, y) + ni(x, y)] \ &= \frac{1}{K} \sum^{K-1}{i=0} f(x, y) + \frac{1}{K} \sum^{K-1}_{i=0} n_i(x, y) \ &\approx f(x, y) \ \end{aligned}$$
      • Background modeling
        • $$B{t+1}(x, y) = \frac{\sum^{K-1}{i=0} wi I{t-i}(x, y)}{\sum^{K-1}_{i=0} w_i}$$
        • $$B_{t+1}(x, y) = (1 - \alpha) B_t(x, y) + \alpha I_t(x, y)$$
  • Image subtraction
    • Enhance difference
    • Usage
      • Change detection
    • Rescaling: ensure pixel values within $$[0, L-1]$$
      • $$g'(x, y) = (g(x, y) - min(g(x, y))) * \frac{L-1}{max(g(x, y)) - min(g(x, y))}$$
  • Multiplication
    • Usage
      • Increase/decrease average gray level
      • Gray-level masks

Convolution

Convolution is symmetric & associative.

$$ f(x) * g(x) = \int^{\infty}_{-\infty} f(u) g(x-u) du

$$

2D Convolution

$$ f(x, y) * g(x, y) = \int^{\infty}{-\infty}\int^{\infty}{-\infty} f(u, v) g(x-u, y-v) dudv

$$

Discrete

$$ f(x) * g(x) = \frac{1}{M} \sum^{M-1}_{u=0} f(u) g(x-u)

$$

$$ f(x, y) * g(x, y) = \frac{1}{MN} \sum^{M-1}{u=0}\sum^{N-1}{v=0} f(u, v) g(x-u, y-v)

$$

Linear Spatial Filtering

Move a mask/filter/kernel over the pixels and retrieve the sum of products.

$$ I2(x, y) = \sum^a{u=-a} \sum^b_{v=-b} w(y, v) I_1(x-u, y-v)

$$

  • Dealing with Borders
    • Limiting the excursions of center of mask
      • Smaller filtered image
    • Paddings (replicating rows & columns)
      • Need a lot of replication if mask is big
    • Partial filter mask: cut the mask if overflowing

Smoothing Filters

Coefficients sum to 1 (no brightness change after applying).

  • Usage
    • Blurring
    • Noise reduction

Sharpening Filters

Accomplished by spatial differentiation. Coefficients sum to 0 (output 0 if no difference).

  • Usage

    • Highlight fine details
    • Enhance details being blurred

Derivatives of a digital function can be obtained by finite differences.

  • $$\frac{\partial I}{\partial x}$$

    • $$I(x+1, y) - I(x, y)$$

    • $$I(x, y) - I(x-1, y)$$

  • $$\frac{\partial^2 I}{\partial x^2}$$

    • $$I(x+1, y) + I(x-1, y) - 2I(x, y)$$

Laplacian Filter

$$\nabla^2 I = \frac{\partial^2 I}{\partial x^2} + \frac{\partial^2 I}{\partial y^2} = [I(x+1, y) + I(x-1, y) + I(x, y+1) + I(x, y-1)] - 4 I(x, y)$$

Composite Laplacian Mask

To preserve background features. Coefficients sum to 1 (copy original information if no difference).

$$g(x, y)=\left{ \begin{array}{c l}
I(x, y) - \nabla^2 I(x, y) & \text{if center coefficient of mask negative}\ I(x, y) + \nabla^2 I(x, y) & \text{if center coefficient of mask positive} \end{array}\right .$$

Nonlinear Spatial Filters

Smoothing Filter

Median Filter

Replace pixel value with median of those in the neighborhood. Effective in removing impulse noise / salt-and-pepper noise. Less blurring than linear smoothing filters.

Order-Statistics Filter

Max Filter

Finding the brightest points. Reducing pepper noise.

Min Filter

Finding the darkest points. Reducing salt noise.

Midpoint filter

Mean of max & min. Reducing randomly distributed noise e.g. Gaussian noise or uniform noise.

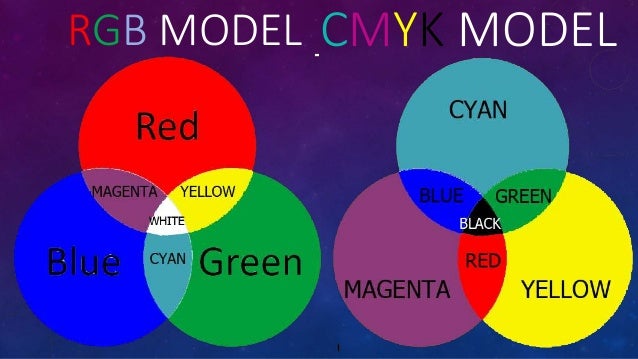
Color Models

  • Primary colors
    • Red
    • Green
    • Blue
  • Secondary colors
    • Cyan
    • Megenta
    • Yello
  • Color models
    • RGB
      • Light-emitting device e.g. color monitors
    • CMY
      • Reflective surface e.g. printers
    • YIQ
      • e.g. color TV broadcast
    • HSI, HSV, etc.

RGB Model

  • Each component represented by 8 bits
    • Pixel depth 24 bits
    • Full-color image
  • Gray scale
    • Equal portions of R, G, B

YIQ Model

$$ \begin{bmatrix} Y \ I \ Q \end{bmatrix} = \begin{bmatrix}

0.299 & 0.587 & 0.114 \ 0.596 & -0.275 & -0.321 \ 0.212 & -0.523 & 0.311 \

\end{bmatrix} \begin{bmatrix} R \ G \ B \end{bmatrix}

$$

  • Y
    • Luminance
      • G larger, similar to human's sense to green light
    • All information required by a monochrome TV set
    • Sum to 1 (no brightness change after applying)
  • I
    • Color information
    • Sum to 0 (no color information if RGB the same)
  • Q
    • Color information
    • Sum to 0 (no color information if RGB the same)

References

results matching ""

    No results matching ""