Multivariate Linear Regression

Linear regression with multiple variables.

Notations

$$x^{(i)}_j$$ = value of feature j in the ith training example

$$x^{(i)}$$ = input features of the ith training example

$$m$$ = number of training examples

$$n$$ = number of features

Hypothesis Equation

$$ \begin{aligned}

h_\theta(x) & = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ... + \theta_n x_n\ & = \begin{bmatrix} \theta_0 & \theta_1 & \dots & \theta_n \end{bmatrix} \begin{bmatrix} x_0\ x_1\ \vdots\ x_n \end{bmatrix}\ & = \theta^Tx

\end{aligned}

$$

Gradient Descent

$$ \begin{align} &\text{Repeat until convergence: {}\

&\hspace{1cm}\thetaj := \theta_j - \alpha\frac{1}{m} \sum^{m}{i=1}{(h_\theta(x^{(i)}) - y^{(i)}) \cdot x^{(i)}_j} \text{ for j := 0...n}\

&\text{}} \end{align}

$$

Gradient Descent in Practice

Feature Scaling

Prefer input variables to be in similar ranges.

Feature Scaling

Divide inputs by range (max - min) or standard deviation to fit then in range $$-1 \le x \le 1$$.

$$ x_i := \frac{x_i}{s_i} \text{ where s_i = range/standard deviation}

$$

Mean Normalization

Subtract average value from input variables to make features approximately zero mean.

$$ x_i := x_i - \mu_i

$$

Combination

$$ x_i := \frac{x_i - \mu_i}{s_i} \text{ where s_i = range/standard deviation}

$$

Learning Rate

Debugging Gradient Descent

Plot number of iterations to J(θ). See if cost function decreases correctly.

Automatic Convergence Test

Declare convergence if J(θ) decreases by less then a small value E e.g. $$10^{-3}$$ in one iteration.

* Fact: if learning rate α is sufficiently small, then J(θ) will decrease on every iteration.

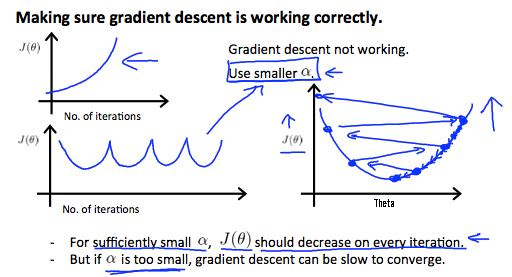
• If α too small: slow convergence
• If α too large: may not decrease on every iteration -> may not converge

Features and Polynomial Regression

Improving Features

Combining multiple features into one.

Polynomial Regression

Change the behavior or curve of h function by making it a quadratic, cubic or square root function (or any other form), to fit the data better.

$$ \begin{align}

h_{\theta}(x) &= \theta_0 + \theta_1x_1 + \theta_2x_1^2\ &= \theta_0 + \theta_1x_1 + \theta_2x_2

\end{align}

$$

* Ranges need to be taken care of for feature scaling.