Trouble Shooting
- Getting more training examples
- Fix high variance
- Trying smaller sets of features
- Fix high variance
- Trying additional features
- Fix high bias
- Trying polynomial features
- Fix high bias
- Increasing λ
- Fix high variance
- Decreasing λ
- Fix high bias
Evaluating Hypothesis
- Split dataset into training (70%) & test (30%) sets
- Learn $$\Theta$$ and minimize $$J_{train}(\Theta)$$
- Compute
- Linear regression
$$ J{test}(\Theta) = \frac{1}{2m{test}} \sum{i=1}^{m{test}} (h{\Theta}(x{test}^{(i)}) - y_{test}^{(i)})^2
$$
- Classification
$$ \begin{aligned} err(h{\Theta}(x), y) &= 1 & \text{ if } h{\Theta}(x) \ge 0.5 \text{ and } y = 0 \text { or } h{\Theta}(x) < 0.5 \text{ and } y = 1 \ &= 0 & \text{otherwise} \ \text{Test error} &= \frac{1}{m{test}}\sum^{m{test}}{i=1} err(h{\Theta}(x^{(i)}{test}), y^{(i)}_{test}) \end{aligned}
$$
Model Selection
- Split dataset into training (60%), cross validation (20%) & test set (20%)
- Learn $$\Theta$$ and minimize $$J_{train}(\Theta)$$ on training set for each polynomial degree
- Find the polynomial degree $$d$$ with the least error using the cross validation set
- Estimate the generalization error using the test set with $$J_{test}(\Theta^{(d)})$$
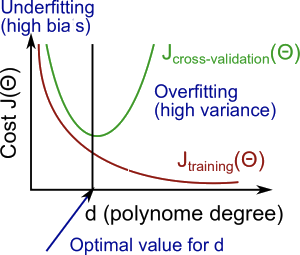
Bias & Variance
High Bias (Underfitting)
- Both $$J{train}(\Theta)$$ & $$J{CV}(\Theta)$$ high
- $$J{train}(\Theta) \approx J{CV}(\Theta)$$
High Variance (Overfitting)
- $$J_{train}(\Theta)$$ low
- $$J{train}(\Theta) \gg J{CV}(\Theta)$$
Regularization
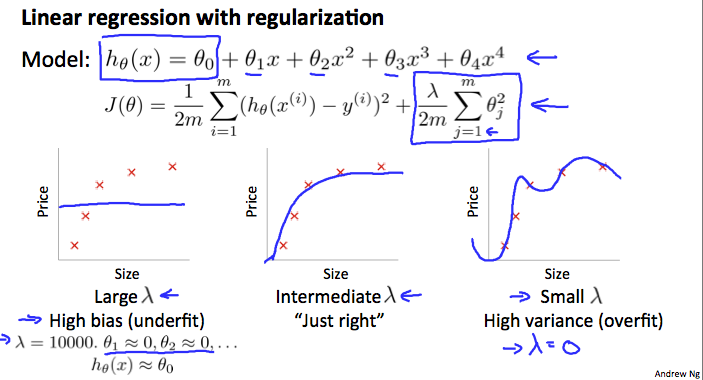
- Create a list of $$\lambda$$ (i.e. $$\lambda \in { 0, 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.64, 1.28, 2.56, 5.12, 10.24 }$$)
- Create a set of models with different degrees or any other variants
- Iterate through the $$\lambda$$ s, and for each one, go through all the models to learn some $$\Theta$$
- Compute the cross validation error using the learned $$\Theta$$ (computed with $$\lambda$$) on the $$J_{CV}(\Theta)$$ without regularization (i.e. $$\lambda = 0$$)
- Select the best combo that produces the lowest error on the cross validation set
- Using the best combo $$\Theta$$ and $$\lambda$$, apply it on $$J_{test}(\Theta)$$ to see if it has a good generalization of the problem
Learning Curves
- As the training set gets larger, the error for a quadratic function increases
- The error value will plateau out after a certain
m, or training set size
High Bias
- Low training set size
- Causes $$J{train}(\Theta)$$ to be low and $$J{CV}(\Theta)$$ to be high
- Large training set size
- Causes both $$J{train}(\Theta)$$ and $$J{CV}(\Theta)$$ to be high
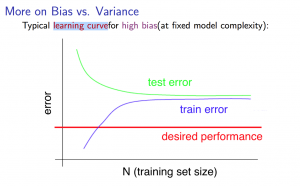
Getting more data will not help.
High Variance
- Low training set size
- Causes $$J{train}(\Theta)$$ to be low and $$J{CV}(\Theta)$$ to be high
- Large training set size
- $$J_{train}(\Theta)$$ increases with training set size
- $$J_{CV}(\Theta)$$ decreases without leveling off
- $$J{train}(\Theta) < J{CV}(\Theta)$$, but difference remains significant
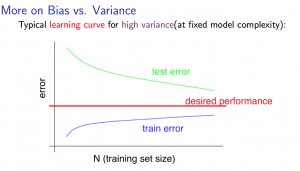
Getting more data will likely help.
Diagnosing Neural Networks
- Few parameters / lower-order polynomials
- Prone to underfitting
- Computationally cheaper
- More parameters / higher-order polynomials
- Prone to overfitting
- Can use regularization (increase λ) to address
- Computationally expensive
- Prone to overfitting
Error Analysis
- Approach to solving ML problems
- Start with a simple algorithm, implement it quickly, test it early on your cross validation data
- Plot learning curves to decide if more data, more features, etc. are likely to help
- Manually examine the errors on examples in the cross validation set, try to spot a trend where most of the errors were made
Skewed Data
| Actual class 1 | Actual class 0 | |
|---|---|---|
| Predicted class 1 | True positive | False positive |
| Predicted class 0 | False negative | True negative |
- Error metrics
- Accuracy
(True positive + True negative) / total examples
- Accuracy
- Precision
True positive / (True positive + False positive)
- Recall
True positive / (True positive + True negative)
- F1-score
2 * precision * recall / (precision + recall)
- Precision