Overfitting

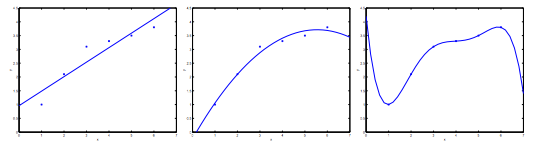
• Underfitting (left)
  • Too simple function, too few features
• Just right (middle)
• Overfitting/high variance (right)
  • Too complicated function, cannot generalize well to predict new data

Solutions

1. Reducing features
   • Manually select which features to keep
   • Use a model selection algorithm
2. Regularization
   • Keep all features, but reduce the magnitude of parameters
   • Works well when we have many slightly useful features

Regularized Linear Regression

Cost Function

Adding regularization term to cost function, $$\lambda$$ being the regularization parameter.

$$ \min{\theta} \frac{1}{2m}\sum^m{i=1} (h\theta(x^{(i)}) - y^{(i)})^2 + \lambda \sum^n{j=1} \theta_j^2

$$

No need to penalize $$\theta_0$$.

Gradient Descent

$$ \begin{align} &\text{Repeat {}\

&\hspace{1cm}\theta0 := \theta_0 - \alpha\frac{1}{m} \sum^{m}{i=1}{(h_\theta(x^{(i)}) - y^{(i)})}x_0^{(i)}\

&\hspace{1cm}\thetaj := \theta_j - \alpha[(\frac{1}{m} \sum^{m}{i=1}{(h_\theta(x^{(i)}) - y^{(i)})}x_j^{(i)}) + \frac{\lambda}{m}\theta_j]\text{ }j\in{1, 2, ..., n}\

&\text{}} \end{align}

$$

or

$$ \begin{align} &\text{Repeat {}\

&\hspace{1cm}\thetaj := \theta_j(1-\alpha\frac{\lambda}{m}) - \alpha\frac{1}{m} \sum^{m}{i=1}{(h_\theta(x^{(i)}) - y^{(i)})}x_j^{(i)})\

&\text{}} \end{align}

$$

where $$(1-\alpha\frac{\lambda}{m})$$ will always be < 1, hence $$\theta_j$$ always decreasing.

Normal Equation

$$ \theta = (X^TX + \lambda \cdot L)^{-1}X^Ty\ where\ L = \begin{bmatrix} 0\ & 1\ & & 1\ & & & \ddots\ & & & & 1 \end{bmatrix} \in \mathcal{R}^{(n+1) \times (n+1)}\

$$

Originally, if $$m < n$$, then $$X^TX$$ non-invertable. If $$m = n$$, may be non-invertable. Adding regularization makes them invertable.

Regularized Logistic Regression

Cost Function

$$ J(\theta) = -\frac{1}{m}\sum^m{i=1}[-y^{(i)} log(h\theta(x^{(i)})) - (1-y^{(i)})log(1-h\theta(x^{(i)}))] + \frac{\lambda}{2m} \sum^n{j=1} \theta_j^2

$$

Gradient Descent

Same as linear regression, instead $$h_\theta$$ is sigmoid function.