Gradient Descent

Estimate the parameters in the hypothesis function.

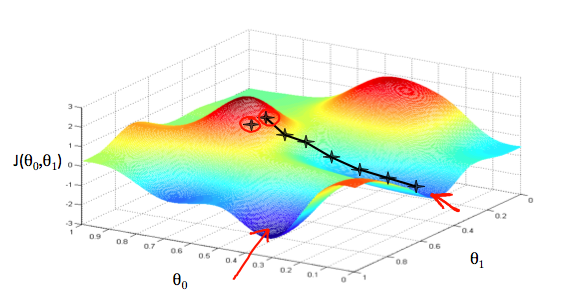
• Make steps down the cost function in the direction with the steepest descent
• The size of each step is determined by the parameter - learning rate α

Algorithm

$$ \theta_j := \theta_j - \alpha\frac{\partial}{\partial \theta_j}J(\theta_0, \theta_1)\ \text{where j represents the feature index number}

$$

Simultaneous Update

$$ t_0 := \theta_0 - \alpha\frac{\partial}{\partial \theta_0}J(\theta_0, \theta_1)\ t_1 := \theta_1 - \alpha\frac{\partial}{\partial \theta_1}J(\theta_0, \theta_1)\ \theta_0 = t_0\ \theta_1 = t_1

$$

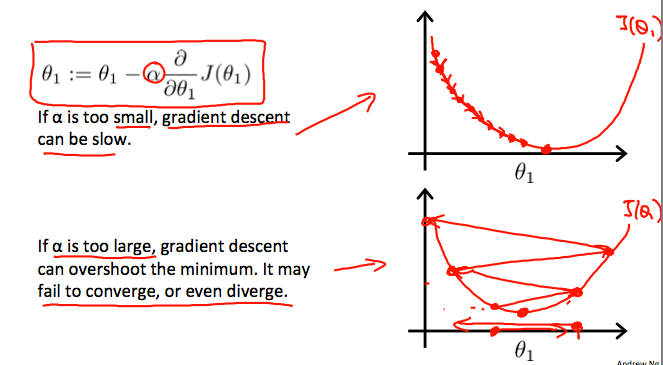
Learning Rate

Gradient Descent for Linear Regression

$$ \begin{align} &\text{Repeat until convergence: {}\ &\hspace{1cm}\theta0 := \theta_0 - \alpha\frac{1}{m} \sum^{m}{i=1}{(h\theta(x^{(i)}) - y^{(i)})}\ &\hspace{1cm}\theta_1 := \theta_1 - \alpha\frac{1}{m} \sum^{m}{i=1}{((h_\theta(x^{(i)}) - y^{(i)})x^{(i)})}\ &\text{}} \end{align}

$$

• Batch gradient descent
  • Looks at every example in the entire training set on every step